Alberto Mesquita Filho
outubro de 2017
Página 7
7.7. Radiação Térmica
Todos os corpos com temperatura acima de 0°K emitem radiação térmica e, em decorrência disso, o espaço está sempre preenchido por essas radiações, até mesmo o mais perfeito dos vácuos que se consegue produzir. Tanto o efeito fotoelétrico (7.3) quanto os espectros de absorção em linhas (7.5) são produzidos pela incidência de feixes de luz provenientes de radiações térmicas, passíveis, como vimos, de uma interpretação condizente com a existência de fótons clássicos (7.4).
As radiações térmicas emitidas pelos corpos nas temperaturas do nosso dia a dia situam-se na faixa do infravermelho, sendo invisíveis para nós. Os gases, por exemplo, emitem essas radiações invisíveis quando em temperaturas do nosso ambiente, e por um processo diferente daquele estudado em 7.5.1: as radiações térmicas não são emitidas pela eletrosfera, mas provavelmente através de um processo de natureza nuclear e associado à energia cinética do átomo como um todo e, portanto, à temperatura. Tratam-se de feixes contínuos, abrangendo uma larga faixa de frequências.
Em virtude das radiações térmicas, corpos em temperaturas elevadas transmitem calor para corpos com temperaturas mais baixas. Corpos com temperaturas iguais, colocados um na vizinhança do outro, e isolados do restante do universo, se mantém em equilíbrio térmico, simplesmente trocando radiações entre si e em quantidades iguais.
7.7.1 Absortividade e/ou emissividade
Seja um corpo qualquer mantido a temperatura constante através do equilíbrio térmico com a vizinhança. Seja Ei a energia da radiação térmica incidente, ou que atinge a superfície unitária do corpo na unidade de tempo e Ea a parte desta energia que é absorvida. O quociente a = Ea/Ei, é chamado absortividade, e retrata a porcentagem da energia incidente que é absorvida. Consequentemente: 0 £ a £ 1. No limite para a = 1 temos o corpo negro ideal [97] (Ea = Ei). O espelho ideal reflete toda a luz incidente, logo a = 0.
Qualquer que seja o caso, para que um corpo se mantenha em temperatura constante, ele deverá perder esta energia absorvida de alguma maneira. Se nenhum outro processo estiver em curso [98], o corpo deverá emitir uma quantidade de energia igual à energia absorvida sob a forma de radiação térmica. Neste caso Ee, a energia emitida por unidade de área e no intervalo de tempo unitário, deverá ser igual a Ea. Consequentemente, Ee = aEi = eEi. Embora a e e sejam idênticos, costuma-se utilizar o símbolo e, a representar a emissividade, quando se está referindo à emissão de energia radiante.
7.7.2 Radiação do corpo negro
Na prática, a radiação oriunda de qualquer cavidade dotada de um pequeno orifício aproxima-se muito da radiação de um corpo negro [99]. Na segunda metade o século XIX, inúmeras foram as tentativas a verificar como deveria se comportar a radiação do corpo negro frente ao que se conhecia na época como física clássica. É oportuno salientar que todos os estudiosos do assunto assumiram a luz como onda eletromagnética. Em decorrência desses estudos, duas leis foram deduzidas, ambas a considerarem a ideia de emissão de luz pelo corpo negro a partir de osciladores harmônicos. Os osciladores harmônicos foram introduzidos por Hertz em 1889 ao descrever a emissão e absorção de ondas hertzianas [100]. As leis deduzidas foram a lei de radiação de Wien e a lei de Rayleigh-Jeans. Não demorou muito para que se demonstrasse a inconsistência dessas leis. É importante repetir que estas leis foram deduzidas frente à hipótese ondulatória e eletromagnética para a luz. Consequentemente, quando se afirma que a física clássica não é capaz de fornecer uma resposta adequada ao problema da radiação de cavidade [101], haja vista que as leis foram falseadas, deve-se entender a frase como pretendendo dizer que o modelo utilizado para a dedução dessas leis foi falseado, mas não a física clássica propriamente dita.
Rubens, Kurlbaum (1898), Lummer e Pringsheim (1896-1901) utilizando-se do artifício cavidade, como corpo negro, mediram a radiação para várias temperaturas em um amplo espectro de comprimento l. Com bases nesses estudos Planck encontrou uma fórmula empírica para a radiância espectral do corpo negro a satisfazer plenamente esses achados experimentais. A fórmula de Planck foi logo substituída por outra mais sofisticada [102] deduzida através da relação entre a entropia e a energia de um conjunto de osciladores harmônicos, supostos responsáveis pela emissão da radiação térmica:
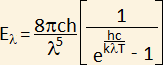 |
(47) |
Nesta fórmula k é a constante de Boltzmann e h é a constante de Planck, a mesma que foi utilizada posteriormente, em 1905, na interpretação do efeito fotoelétrico (7.3) por Einstein.
Seja então El a radiância espectral, definida pela quantidade de radiação emitida pela superfície de um corpo em um intervalo de comprimento dl a uma temperatura T e por unidade de tempo. O gráfico obtido experimentalmente por Lummer e Pringsheim para a função El = f(l) do corpo negro é muito semelhante [103] àquele mostrado na figura 78, construído a partir da equação 47.

Figura 78: Radiância espectral do corpo
negro em função da temperatura.
A fórmula de Planck representou uma tentativa de salvar o modelo dos osciladores harmônicos, ainda que a um preço bastante elevado, e os adeptos da física quântica que o digam [104]. Não há como questionar a fórmula pois, como exposto acima, ela atende plenamente ao que é observado na experimentação. Pensando-se em luz material um dos problemas reside em se chegar à fórmula observando a ideia de fóton clássico. O caminho não é fácil e está além dos objetivos propostos para este artigo.
Muitos assuntos ficaram pendentes, em especial, mas não só, aqueles relacionados à radiação térmica e a como ela se processa. Certamente o movimento vibratório e/ou a energia cinética dos átomos e moléculas desempenha um papel essencial ao processo, mas isto por si só não explica, por exemplo, o porquê dos fótons clássicos terem um comprimento L constante, como observado em 7.4. Também não explica a irreversibilidade termodinâmica, um dos objetivos do trabalho de Planck e que, na época, também resultou inconclusivo. Há que se explicar também como seriam as órbitas dos elétrons compatíveis com as ideias aqui expostas. Ao afirmarmos que a luz é material, toda a física da atualidade deve se adaptar a esta realidade e este é um assunto a ser compartilhado por milhares de artigos produzidos não apenas por um, mas por centenas ou milhares de autores. Citarei apenas alguns de minha autoria e/ou diálogos que participei, e que estão publicados no Espaço Científico Cultural:
Sobre a mecânica clássica: 1) O movimento absoluto e a física de Newton; 2) O Modelo Mecânico Newtoniano ou Clássico; 3) Da física antiga à física moderna; 4) A Quintessência do Universo (diálogo); 5) Considerações Sobre o Tempo (diálogo); 6) Explicação clássica para a experiência da dupla fenda; 7) Como é que um campo imaterial pode interagir com a matéria.
Sobre a relatividade: 1) A relatividade galileana; 2) O Espaço Curvo Euclidiano e a Relatividade Galileana; 3) O fenômeno luz e as falácias relativas às relatividades; 4) Eletromagnetismo e Relatividade; 5) Velocidades superluminais; 6) O paradoxo da carga acelerada (diálogo); 7) O Paradoxo dos Trigêmeos; 8) Einstein Equivalence Principle is wrong? (diálogo); 9) Einstein-Faraday's Elevator; 10) Relatividade em duas dimensões - Um novo paradoxo.
Sobre a teoria quântica: 1) Sobre as origens da física moderna; 2) A energia da física moderna; 3) A natureza da luz e o princípio da superposição; 4) Questionando a física quântica (diálogo); 5) Considerações sobre a Incerteza; 6) Teorias Realistas Atuais e o Paradoxo EPR (diálogo); 7) Sobre a natureza íntima da matéria (diálogo); 8) O spin que não é giro.
Sobre o eletromagnetismo clássico: 1) Um elétron não tão nebuloso; 2) A equação do elétron e o eletromagnetismo; 3) Sobre a natureza físico-matemática do Elétron; 4) O Elétron Emissor de Informações Eletromagnéticas; 5) Similaridades entre Campos de Velocidade e o Campo Eletromagnético; 6) Elétron e Carga Elétrica (diálogo)
Sobre a termodinâmica: 1) Variáveis Escondidas e a Termodinâmica; 2) Velas Solares: Furadas? (diálogo); 3) Calor específico e física clássica.

 Para
continuar a leitura clique na figura à direita Þ
Para
continuar a leitura clique na figura à direita Þ
Ü Para retornar, clique na figura à esquerda.