A Estrutura da Luz e a Interação Luz-Matéria

Alberto Mesquita Filho     
outubro de 2017
Página 6

Índice deste artigo

7.5 Absorção e emissão de luz pelo átomo de hidrogênio

Os gases em baixa pressão ou baixa densidade absorvem ou emitem raios de luz de apenas determinadas frequências n. Se um feixe de luz contínua (proveniente do sol ou de uma lâmpada incandescente) atravessar estes gases, os raios com estas frequências serão absorvidos. Se colocarmos um prisma no trajeto do feixe transmitido obteremos, em um anteparo, um espectro de absorção em linhas, a caracterizar a ausência dos raios que foram absorvidos (figura 70, imagem do anteparo colocado mais à esquerda).

Figura 70: Espectros de absorção e de emissão do gás hidrogênio.

Retirando-se a fonte de luz contínua, e utilizando um equipamento bem mais sensível, obteremos no anteparo o espectro de emissão do gás (figura 70 à direita). Neste caso o gás está funcionando como fonte da luz que aparece no anteparo. No mesmo local em que apareciam estrias denunciando a absorção, aparecerão agora estrias denunciando a emissão. Os dois espectros (absorção e emissão) são, portanto, complementares. Os raios que antes eram totalmente absorvidos pelo gás e reemitidos em todas as direções, com o consequente enfraquecimento destes na direção do feixe transmitido, são agora evidenciados no espectro de emissão, graças à maior sensibilidade do equipamento e a ausência dos raios da luz normal.

Como explicar este fenômeno? A situação é um pouco diferente daquela observada com placas metálicas. Todos os raios de luz observados em 7.3 e com uma frequência superior a um determinado valor n_o eram absorvidos por um elétron; e é provável que os outros também sejam absorvidos, apesar de não ocasionarem a ejeção do elétron pelo fato da energia ser insuficiente para tal. Agora existe uma seletividade. Apenas raios de certas frequências bastante específicas são absorvidos ou emitidos. A especificidade é tal que se presta a caracterizar a natureza do gás, assim como as impressões digitais servem para identificar uma pessoa. Para o caso do hidrogênio esses raios são tais que os comprimentos l são dados pela expressão empírica (fórmula de Rydberg):

		(37)

R é a constante de Rydberg (0,00109737 Å^-1) e n₁ e n₂ são inteiros positivos tal que n₁ = 1, 2, 3... e n₂ > n₁ [78]. Na tabela 3 temos os valores de l obtidos da equação 37 para n₁ = 2 (série de Balmer) e na faixa do espectro visível.

Utilizando a expressão que relaciona l a n (equação 25) obtemos a fórmula de Rydberg em termos da frequência n:

		(38)

7.5.1 O modelo de Bohr para o átomo de hidrogênio

Uma explicação bastante convincente para este achado experimental foi encontrada por Bohr [79] em 1913. Bohr assumiu o modelo de Rutherford para o átomo de hidrogênio, com o elétron circulando ao redor do núcleo (próton). Este elétron, ao absorver um fóton de frequência n, saltaria para uma órbita mais externa, como mostra a figura 71; e ao emitir um fóton semelhante, retornaria ao estado inicial.

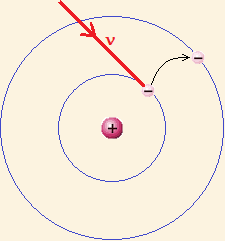
Figura 71: Transição entre dois estados estacionários
do átomo de hidrogênio, segundo Bohr..

Afim de justificar o modelo de Rutherford frente aos achados experimentais (fórmula de Rydberg) e às teorias clássicas vigentes (mecânica newtoniana e eletromagnetismo de Maxwell-Lorentz), Bohr sentiu-se compelido a assumir dois postulados [80]. Vamos então começar por uma das afirmações contida no segundo postulado [81] e a dizer que a frequência n, quando o elétron salta de uma órbita para outra mais externa, é dada por

onde h é a constante de Planck. E_i e E_f são os valores da energia do átomo nos dois estados estacionários (inicial e final) do processo de radiação.

Mas hn, segundo a fórmula de Rydberg (equação 38), pode ser escrito como:

		(40)

Bohr conclui [82] então que a energia total do átomo, em cada um de seus estados estacionários, pode ser escrita como

		(41)

O valor de E_n pode ser deduzido das teorias clássicas. Considerando o próton fixo no centro do átomo, a energia total do átomo é dada por

E_n = Energia cinética do elétron + Energia potencial do par elétron-próton.

A mecânica newtoniana fornece o primeiro termo e o eletromagnetismo de Maxwell-Lorentz [83] fornece o segundo. Matematicamente está tudo muito bem encaixado e fisicamente consegue-se evoluir por esta linha graças a experiências executadas na época de Bohr e que trouxeram à luz as propriedades do elétron inseridas nestas fórmulas. Há, não obstante, dois sérios problemas a serem justificados por quem quer que pretenda seguir este procedimento.

O primeiro consiste em explicar porque o elétron só pode se situar em estados estacionários especiais ou peculiares, como afirma Bohr (relacionados a um número inteiro n). O que impede o elétron de se situar em órbitas que não satisfaçam a inteireza de n? Ou então, porque a energia do átomo é “quantizada”, como mostra a equação 41? Alguns autores chegam a chamar as órbitas que satisfazem a inteireza de n como “órbitas permitidas”, dando a entender que órbitas com raios diferentes seriam “órbitas proibidas”. Isso é muito estranho em termos de mecânica clássica! Bohr conclui então que o comportamento do átomo satisfaz apenas parcialmente a mecânica newtoniana, propondo, em seu primeiro postulado [84], a ideia de “quantização”, como algo a ser explicado com o desenvolvimento de sua teoria. O elétron então saltaria de uma órbita para outra, ou de um estado estacionário para outro, sem passar pelos estados intermediários.

O segundo problema associa-se à teoria de Maxwell, a prever que uma carga elétrica acelerada deve emitir radiação eletromagnética, fato este comprovado experimentalmente por Hertz, como vimos em 7.3. Ora, aceitando-se a expansão feita por Lorentz ao eletromagnetismo de Maxwell [83], um elétron dotado de aceleração centrípeta (elétron em órbita) deveria sempre emitir radiação eletromagnética. Com isso ele iria perdendo energia gradativamente, caindo rapidamente no núcleo. Bohr conclui então que o comportamento do átomo também satisfaz apenas parcialmente o eletromagnetismo de Maxwell-Lorentz. Ou seja, propõe agora através do postulado 2 [81], que nos estados estacionários o elétron não obedeceria a previsão da teoria de Maxwell acima citada, emitindo radiação eletromagnética apenas quando salta de um estado estacionário para outro.

Muito mais poderia ser dito mas vou parar por aqui pois o que temos já é suficiente para confrontarmos a teoria de Bohr com a proposição de luz material.

7.5.2 Primeiras críticas à teoria de Bohr

Entre a publicação da teoria de Bohr e a sua plena aceitação pela comunidade científica, inúmeras críticas vieram à tona [85]. Digna de nota foi a objeção de Oseen, amigo e colega de Bohr, interessado em saber como a teoria de Maxwell-Lorentz deveria ser modificada para permitir a existência de um átomo do tipo proposto [86]. Schott, por outro lado, concluiu, após longos cálculos, que os postulados de Bohr eram de fato inconsistentes com a eletrodinâmica ordinária e só poderiam ser salvos por uma modificação astuciosa da teoria [86]. Ao que parece a objeção de Oseen foi ignorada e a sugestão de Schott, salvo melhor juízo, se traduziu na evolução do modelo de Bohr, baseado na mecânica quântica primitiva, para a teoria quântica atual.

Frente à ideia de luz corpuscular há que se reconsiderar o argumento de Oseen, porém com algumas ressalvas. Com respeito à genuína teoria de Maxwell não me parece ser prudente promover modificação alguma, haja vista que ela tem se mostrado totalmente consistente dentro de sua área de atuação, ou seja, tem cumprido com as finalidades para as quais foi projetada. Quando muito, poderíamos questionar seus limites operacionais e/ou as dimensões nas quais a teoria é válida. Não obstante, a teoria de Bohr, como vimos acima, utilizou a síntese promovida por Lorentz entre a teoria de Maxwell e a concepção atômica da matéria [87]. Lorentz adotou uma hipótese aceita consensualmente em sua época, a de que o elétron é uma carga elétrica em miniatura [88]. Quero crer que qualquer modificação no eletromagnetismo de Maxwell-Lorentz deva começar pelo questionamento dessa hipótese. Vejamos então até que ponto seria possível compatibilizar esses átomos da eletricidade [89] com o fóton clássico apresentado nos itens anteriores.

7.6. Sobre a natureza do elétron

Aceitando a percepção newtoniana de que corpos materiais e luz são convertíveis um no outro, podemos conjecturar a respeito de como deveriam se processar estas conversões luz « matéria (absorção e emissão de luz). A questão, então, seria a seguinte: Como seria a natureza de um elétron para que ele pudesse incorporar ou emitir um fóton clássico, como aquele aqui proposto? Em condições especiais, esta conversão chega a ser total. Por exemplo, na produção de pares elétron-pósitron, um único fóton [90] se desdobra nessas duas partículas. O fóton desaparece e em seu lugar surgem duas partículas gêmeas. Ou seja, o elétron tem muito em comum com o fóton clássico. Isto leva-nos a concluir que o elétron deva ser constituído exclusivamente por corpúsculos de luz e, de alguma maneira, consegue incorporar à sua estrutura os fótons que absorve.

Não é nenhum absurdo pensar que a absorção resulte do enrolamento total de um fóton clássico na estrutura do elétron, enquanto que na emissão haveria um desenrolamento parcial do elétron. Digno de nota é o fato de que todos os fótons têm o mesmo comprimento L, como demonstramos em 7.4 e, utilizando uma verificação efetuada por Newton, concluímos que esse comprimento não pode ser inferior a 0,0625m. Já o elétron costuma ser considerado uma partícula puntiforme ou, quando muito, como uma nuvem espalhada na periferia do átomo [91]. Porém, antes de lançar conjecturas de como poderia se dar esse possível enrolamento, ou desenrolamento, vamos interpretar mais alguns dados experimentais frente à aceitação da natureza corpuscular para a luz.

7.6.1 O elétron clássico e a fórmula de Rydberg

Quando o elétron salta de seu estado fundamental (n=1 ou primeira órbita) para outro estado qualquer (n=n ou enésima órbita), ele pode fazer isso de várias maneiras. Vamos considerar duas:

em n-1 etapas, passando pelas órbitas 2, 3, 4... etc., até atingir n;

ou saltando diretamente da órbita 1 para a órbita n.

No primeiro caso ele irá incorporar n-1 fótons cujos comprimentos l serão representados por l₁₂, l₂₃, l₃₄, ... l_(n-1)n, enquanto que no segundo caso irá incorporar apenas um fóton com l = l_1n. O número de corpúsculos de luz N que o elétron irá receber ao incorporar cada um dos fótons pode ser calculado pela equação 36, qual seja: N = 2L/l. Para a transformação total teremos, no primeiro caso (salto por etapas):

		(42)

ou

enquanto que no segundo caso teremos:

		(43)

Substituindo os 1/l’s das equaçôes 42 e 43 pelos valores dados pela fórmula de Rydberg (37) temos:

De 42:

De 43:

		(44)

Portanto:

		(45)

A equação 44 pode ser generalizada para outros saltos, iniciando em outras órbitas (2, 3, etc.), através da equação

		(46)

podendo-se verificar também a identidade (45) para saltos por etapas iniciando em uma órbita i qualquer e terminando em outra órbita j qualquer.

O resultado ora apresentado é totalmente compatível com a admissão de uma propriedade do elétron variável para cada um dos possíveis estados estacionários descritos por Bohr. E que propriedade seria essa se não a sua massa? Afinal o elétron está incorporando corpúsculos materiais entre um estado e outro, e qualquer que seja a via utilizada, o número de corpúsculos que incorpora depende apenas do estado inicial e final do processo. O elétron não deve, portanto, ter massa constante, como costumeiramente se admite, mas a sua massa deve variar por um valor que pode ser muito pequeno, mas provavelmente nem sempre desprezível para efeitos de cálculos. Em que condições seria desprezível? A equação 46 fornece a resposta. O número de corpúsculos N absorvidos em um salto é função apenas de n_i e n_j, pois L e R são constantes. De acordo com o gráfico da figura 72, para saltos a partir da órbita fundamental (i=1) para a órbita imediatamente seguinte (j = i+1), N/2LR e, consequentemente N, decresce rapidamente. A partir da quinta ou sexta órbita, seu valor é quase nulo quando comparado com os valores anteriores. Nestas condições tudo se passa como se a massa do elétron permanecesse constante e, consequentemente, as equações que utilizam a constância da massa serão aproximadamente válidas. Este é o território em que se costuma dizer que as equações da mecânica clássica são válidas [92]. E tanto são válidas que foi nestas condições (grandes órbitas) que se determinou a fórmula que dá o valor da constante de Rydberg utilizando-se equações da mecânica clássica.

Figura 72: Explicação no texto

7.6.2 O elétron girante

Voltemos agora à questão de como se dá o enrolamento de um fóton clássico na estrutura do elétron. Já vimos o quanto esse fóton deve encolher devido ao enrolamento. Ocorre-me então duas possibilidades, e o leitor fica convidado a apresentar uma terceira, se é que exista.

Poderíamos pensar em algo do tipo do enrolamento de uma linha em um carretel, e o carretel tendo o formato de um toroide, como mostra a figura 73a. Este suposto elétron seria então constituído exclusivamente por corpúsculos de luz trafegando segundo uma espiral toroidal como mostra a figura 73b. Os corpúsculos dispõem-se em duas colunas, cada uma com corpúsculos do mesmo tipo (giros coincidentes).

                        
                                               Figura 73: Explicação no texto

O fóton, para entrar na estrutura deste elétron, vai encaixando seus corpúsculos um a um, no intervalo entre dois corpúsculos contíguos (figura 73b e c). Notar a existência de duas rotações além daquela própria aos corpúsculos de luz. A rotação de cada corpúsculo segundo o eixo da espiral, como mostrado na figura 73b (seta circular vermelha); e a rotação do conjunto como um todo (rotação do elétron), à medida que esse conjunto de corpúsculos progride através da espiral.
 

Outra imagem para o elétron, talvez mais profícua que a anterior, seria a de um anel girante, como mostra o gif animado a seguir (figura 74). O anel seria constituído por corpúsculos de luz como mostra a figura 75 [93]. Ao contrário do fóton clássico, neste elétron os corpúsculos contíguos giram no mesmo sentido e com os giros acoplados, ou emparelhados. Além do giro próprio aos corpúsculos, existem outros dois giros, como no caso anterior.

Figura 74: gif animado	Figura 75: Explicação no texto

Um destes giros seria dos corpúsculos em relação ao aro, ou anel; o outro seria do aro, ou do conjunto como um todo (rotação do elétron). Utilizarei o símbolo w para identificar o momento angular correspondente a este giro do elétron. Qualquer semelhança com o spin quântico é mera coincidência, haja vista que estamos falando de um elétron clássico e, portanto, de um giro real. A figura 76 mostra como se dá o lançamento de fótons clássicos, pelo equador do elétron. Neste caso o comprimento l do fóton está relacionado ao diâmetro equatorial do elétron e ao momento angular w. Observa-se também uma relação entre w e a velocidade da luz c. São estes relacionamentos entre o giro w do elétron (ou o giro principal do sistema) com as propriedades da luz que tornam este segundo modelo mais profícuo do que o anterior, como assinalado acima. Veremos abaixo, e também no item 8, mais detalhes a esse respeito, relacionados a propriedades eletromagnéticas desse elétron.

Figura 76: Explicação no texto

7.6.3 O elétron clássico e o eletromagnetismo

Não há como imaginar que elétrons girantes, como aqueles mostrados em 7.6.1, fossem capazes de gerar campos elétricos de simetria esférica (campo de Coulomb). Nenhuma experiência até hoje comprovou explicitamente a semelhança entre o elétron e a carga elétrica de Coulomb. Quando muito, o que se demonstrou experimentalmente, no início do século XX, foi que o elétron responde a campos elétricos e magnéticos da teoria de Maxwell de maneira semelhante a uma carga elétrica [94], mas não que gera um campo semelhante àquele a que está se sujeitando nestas experiências. De fato, o elétron, assim como o próton, é a partícula elementar ou fundamental do eletromagnetismo, assim como as moléculas são partículas fundamentais no estudo dos fluidos. Não obstante, assim como a mecânica dos fluidos foi construída sem utilizar a noção de molécula, o eletromagnetismo foi construído sem utilizar a noção de elétrons e prótons. As duas teorias caracterizam um artefato chamado elemento de volume, considerando-o como a unidade morfológica destes modelos teóricos. Esta unidade morfológica sim, é idêntica aos elementos macroscópicos, e os modelos funcionam; e tanto funcionam que quase toda a tecnologia do século XX tem por base modelos como estes. Apesar dos modelos funcionarem, seus elementos de volume têm uma forma matematicamente adaptável ao que se pretenda demonstrar; representam objetos macroscópicos de dimensões ínfimas, mas não partículas elementares reais. Sabemos hoje que a molécula de água não é amorfa e, por motivos idênticos, podemos desconfiar que os elétrons e os prótons também não sejam estruturalmente semelhantes aos elementos de volume da teoria de Maxwell.

Em vista do exposto, é lógico admitir que o campo eletromagnético de um elétron esteja associado ao vetor w que caracteriza o seu giro. Este campo deverá, de alguma maneira, produzir os campos E e B da teoria de Maxwell sempre que os elétrons se dispuserem, nos condutores, de forma a constituírem uma carga ou uma corrente elétrica da teoria de Maxwell. Essas disposições estão representadas na figura 77a para a carga elétrica e na figura 77b para a corrente elétrica.

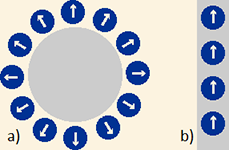
Figura 77: Explicação no texto

Se definirmos um vetor potencial eletromagnético A para o elétron através da expressão A = w/r, e assumirmos o campo elétrico do elétron dado por x = (Ñ.A)v [em que Ñ.A é a divergência de A e v é um vetor unitário correspondente ao vetor w] obteremos, pela integração dos x’s de elementos de superfície da esfera representada na figura 77a, uma expressão idêntica àquela observada por Coulomb para o campo elétrico E [95]. Por outro lado, se assumirmos que o campo magnético desse elétron é dado por b = Ñ×A, [Ñ×A é o rotacional de A], expandindo essa expressão não é difícil verificar que b, expresso em função de r, é idêntico ao campo magnético dB de um elemento de corrente dado pela lei de Biot-Savart [96].

Dou então por concluída a tarefa imposta na última frase do subitem 7.5.2. Com respeito à objeção de Oseen (7.5.2) mostramos como a teoria de Maxwell-Lorentz poderia ser modificada, faltando justificar o fato deste elétron clássico não emitir radiação quando acelerado nas condições impostas por Bohr. Esta associação entre aceleração e emissão de radiação é válida para as cargas elétricas macroscópicas da teoria de Maxwell. No caso do elétron pode-se demonstrar que a emissão de radiação ocorrerá apenas quando a aceleração estiver associada a um aumento no módulo do vetor w (ou da intensidade do giro), o que não ocorre no caso assinalado (estados estacionários de Bohr). A demonstração está além do escopo deste artigo.

Para continuar a leitura clique na figura à direita Þ

Ü Para retornar, clique na figura à esquerda.